Em uma era impulsionada pela informação e interconexão, a descoberta de padrões nas conexões desempenham um papel crucial em nossa compreensão de sistemas complexos. Nesse contexto, os grafos emergem como uma ferramenta matemática poderosa, capaz de representar e analisar essas intrincadas conexões. No mundo dos grafos, os simples pontos e linhas ganham vida, revelando insights profundos em campos tão diversos quanto redes sociais e logística, biologia e tecnologia da informação.
As Estruturas Fundamentais de um Grafo
Em sua essência, um grafo é uma representação visual e matemática de um conjunto de objetos e das conexões entre eles. Os objetos em questão são chamados de “vértices” (ou “nós”), e as ligações que unem esses vértices são denominadas “arestas”. A simplicidade dessa estrutura é o que torna os grafos tão versáteis e poderosos.
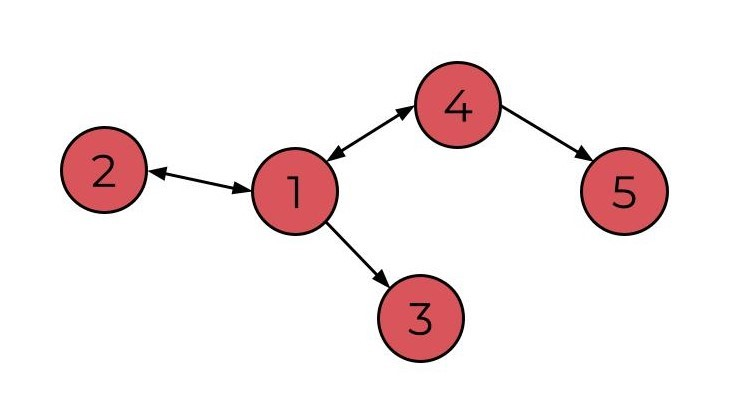
Vértices são os pontos essenciais em um grafo, representando entidades ou elementos individuais que podem estar interconectados de alguma forma. Por exemplo, em uma rede social, cada perfil de usuário pode ser representado por um nó, e em um sistema de gerenciamento de estradas, cada cruzamento pode ser considerado um nó. No exemplo abaixo pode ser observado 5 Nós.
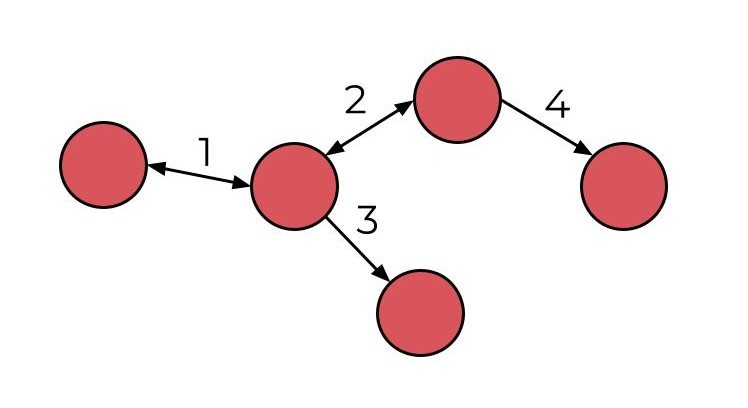
As arestas são as conexões entre nós, representando as relações entre eles. Essas conexões podem ser direcionadas ou não direcionadas, dependendo se a relação é unidirecional ou bidirecional. Em contextos de redes sociais, uma aresta pode indicar uma amizade entre dois usuários, enquanto em um mapa rodoviário, uma aresta ligaria dois cruzamentos adjacentes. No grafo abaixo há 4 arestas sendo duas bidirecionais e as outras duas unidirecionais.
Tipos de Grafos
Existem dois tipos fundamentais de grafos que formam a base para a maioria das aplicações:
Grafos Não-Direcionados: Nestes grafos, as arestas que conectam os vértices não possuem uma direção específica, ou seja, a relação entre dois vértices é bidirecional. Por exemplo, pense em um grafo não-direcionado que represente amizades em uma rede social. Se A é amigo de B, isso implica que B também é amigo de A.
Grafos Direcionados (ou Digrafos): Ao contrário dos grafos não-direcionados, em um grafo direcionado, as arestas têm uma direção específica, o que significa que a relação entre os vértices é unidirecional. Por exemplo, em um grafo direcionado que represente seguidores em uma rede social, se A segue B, isso não implica necessariamente que B segue A.
Algoritmos para análise de grafos
Além de entender a estrutura dos grafos, é crucial explorar os algoritmos que nos permitem extrair informações valiosas dessas representações. Aqui estão alguns algoritmos-chave:
- Busca em Largura (Breadth-First Search – BFS): Este algoritmo é fundamental para a exploração de grafos do tipo árvore e, particularmente, para encontrar o caminho mais curto entre dois nós. Inicia a busca a partir do nó de origem, movendo-se gradualmente para nós vizinhos antes de prosseguir para nós mais distantes. Imagine sua aplicação na navegação de mapas urbanos para encontrar a rota mais curta entre dois locais.
- Busca em Profundidade (Depth-First Search – DFS): Contrariamente ao BFS, o DFS explora tão profundamente quanto possível antes de retroceder. É útil para identificar componentes conectados em um grafo e para resolver problemas de backtracking, como a resolução de labirintos.
- Algoritmo de Dijkstra: Utilizado para encontrar o caminho mais curto em um grafo ponderado, onde as arestas têm valores associados. É aplicado em sistemas de navegação, otimização de rotas e redes de transporte. Pense em um aplicativo de navegação que calcula a rota mais rápida entre dois pontos, levando em consideração o tráfego em tempo real.
- Algoritmo de Kruskal: Este algoritmo é usado para encontrar a árvore geradora mínima em um grafo ponderado, com o objetivo de conectar todos os nós com o mínimo custo possível. É aplicado em problemas de otimização, como o projeto de redes de cabos, para minimizar os custos de instalação.
- Algoritmo de Floyd-Warshall: Utilizado para encontrar todos os caminhos mais curtos entre todos os pares de nós em um grafo, considerando arestas ponderadas. Essa técnica é amplamente utilizada na análise de redes de transporte e infraestrutura para calcular as distâncias mais curtas entre várias localizações.
Aplicações
Os grafos podem ser utilizados em diferentes desafios práticos. Aqui estão exemplos onde é aplicada com sucesso esta metodologia:
- Redes Sociais e Análise de Mídia Social: Grafos são utilizados para representar redes sociais, onde os nós representam perfis de usuários e as arestas indicam conexões de amizade. A análise de grafos pode identificar comunidades, influenciadores-chave e detectar campanhas de spam.
- Recomendação de Conteúdo: Plataformas como Netflix e Amazon utilizam algoritmos de grafos para recomendar conteúdo com base nas interações dos usuários com filmes, produtos e classificações anteriores.
- Redes de Colaboração Acadêmica: Grafos são usados para modelar redes de colaboração entre cientistas, ajudando a identificar especialistas em campos específicos e tendências de pesquisa.
- Detecção de Fraude e Análise de Risco: Grafos são empregados na detecção de fraudes, como a fraude em cartões de crédito, identificando padrões de transações suspeitas e conexões anômalas.
- Sistemas de Recomendação de Rotas e Logística: Em logística e transporte, os grafos otimizam rotas de entrega, minimizam custos e evitam congestionamentos.
- Biologia e Genética: Na biologia, grafos representam interações entre proteínas, genes e moléculas, auxiliando na compreensão de redes biomoleculares.
Esses exemplos demonstram como os grafos são uma ferramenta essencial na ciência de dados, permitindo a análise, visualização e tomada de decisões com base em relações complexas. À medida que a ciência de dados evolui, os grafos se tornam ainda mais valiosos na extração de insights de dados interconectados.
Na Murabei, estamos desenvolvendo soluções e modelos com base em grafos para vários desafios importantes de nossos clientes. Acreditamos que os grafos não são apenas teoria, mas uma ferramenta essencial – e bonita- para analisar dados do mundo real.
Autor: Lucas Cardoso
Conheça um pouco mais do jeito Murabei acompanhando nosso perfil no Linkedin.