The Earth was small, light blue, and so touchingly alone, our home that must be defended like a holy relic. The Earth was absolutely round. I believe I never knew what the word round meant until I saw Earth from space.
Alexey Leonov
Última atualização: 31/07/2020
Metodologia: Cálculo da distância entre os centróides
O objetivo dessa passagem é pré calcular as distâncias entre os centróides dos setores censitários do IBGE. Para fazer esse cálculo devemos primeiro lembrar que a terra é redonda (na verdade não, mas também não é plana), dessa forma para calcular a distância entre os pontos temos que “caminhar” na curvatura da terra (Fig. 1).
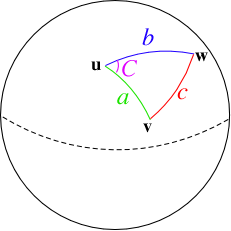
Para para fazer essa caminhada matemática temos que utilizar a fórmula de Haversine, na qual é calculada a distância em graus entre dois pontos em uma esfera. Depois disso podemos converter em km utilizando como base o diâmetro da terra (12,742 km).
Para a conversão de graus em Km, o que facilita muito a análise visto que é difícil pensar distância em graus, vamos utilizar fórmulas básicas do raio do círculo. Considerando que a terra no equador é um círculo (aproximadamente) e lembrando um pouco do 2o colegial, temos:
Substituindo com o diâmetro da terra:
Considerando que são 360 graus para uma volta completa, podemos calcular quantos km temos que andar para corresponder à um grau na superfície da terra.
Dessa forma temos todos os elementos para calcular as distâncias entre os centróides dos setores censitários. Para o cálculo devemos considerar a quantidade de dados que serão gerados se cruzarmos todos os centróides disponíveis na base do IBGE. No total temos 316.575 setores censitários, assim se fizermos o cruzamento de todos contra todos teremos um total de 100.219.730.625 linhas na nossa base de dados de distâncias.
Considerando que vamos demorar cerca de 0.01 segundos para fazer cada um dos cálculos e salvar, então demoraremos 100.219.730.6,25 segundos, que são 16.703.288 minutos, que são 278.388,1 horas, que são 11.599,5 dias, que são 32.22 anos… É, acho que não vamos esperar 32 anos só para ter uma base de distâncias de centróides para então fazermos a análise sobre qual foi o efeito da quarenta sobre o deslocamento de pessoas.

Uma solução para o problema acima é reduzir a amostra, vamos calcular as distâncias para os centróides que sejam distantes menos de 25km. Essa distância abarca por exemplo o raio do centro de São Paulo e a maior parte da região metropolitana..
Outra estratégia é paralelizar o processo, isso significa que são feitos diversos cálculos ao mesmo tempo. Essa metodologia é amplamente utilizada nas placas de vídeo utilizadas tanto nos jogos de videogame última geração como em modelo de inteligência artificial. Abaixo segue o código utilizado para gerar a combinação de distâncias, utilizando como base os centróides calculados no passo anterior.
to_process = all_shapes[["sector_code_ibge", "centroid", "lat", "lon"]]
results = []
# Transforma o dataframe em uma lista de dicionários para que possam ser
# processados de forma paralela
dict_data = to_process.to_dict("records")
to_pool = [{"row": x, "dataset": to_process} for x in dict_data
# para utilizar o pool é necesário definir uma função para que rode
# sobre os elementos do dicionário
def f(args):
row = args["row"]
file_path = "{sector_code_ibge}__distance.csv".format(
sector_code_ibge=row["sector_code_ibge"])
# faz o processo de forma incremental, assim se esse setor já
# foi processado anteriormente ele não é processado
if os.path.isfile(file_path):
print("skiping: ", file_path)
return None
print("start: ", file_path)
dataset = args["dataset"]
centroid = row["centroid"]
# Calcula a distancia em km utilizando a aproximação da terra
# esférica
distance_km = dataset[
"centroid"].map(lambda x: x.distance(centroid))*111.2
# Limita os dados para aqueles que tem menos de 25km de distância
to_add = dataset[distance_km <= 25].copy()
del to_add["centroid"]
to_add["sector_code_ibge_ref"] = row["sector_code_ibge"]
to_add["lat_ref"] = row["lat"]
to_add["lon_ref"] = row["lon"]
to_add["distance"] = distance_km[distance_km <= 25]
to_add.to_csv(file_path, index=False)
print("end: ", file_path)
# Define um pool para que rode 20 processos em paralelo
p = Pool(20)
all_results = p.map(f, to_pool)Com o código acima foi possível obter as distâncias para os centroides de distância inferior à 25km em um dia de cálculo. A base foi posteriormente agregada e utilizada para a criação de uma base de dados à ser utilizada no estudo de distância.