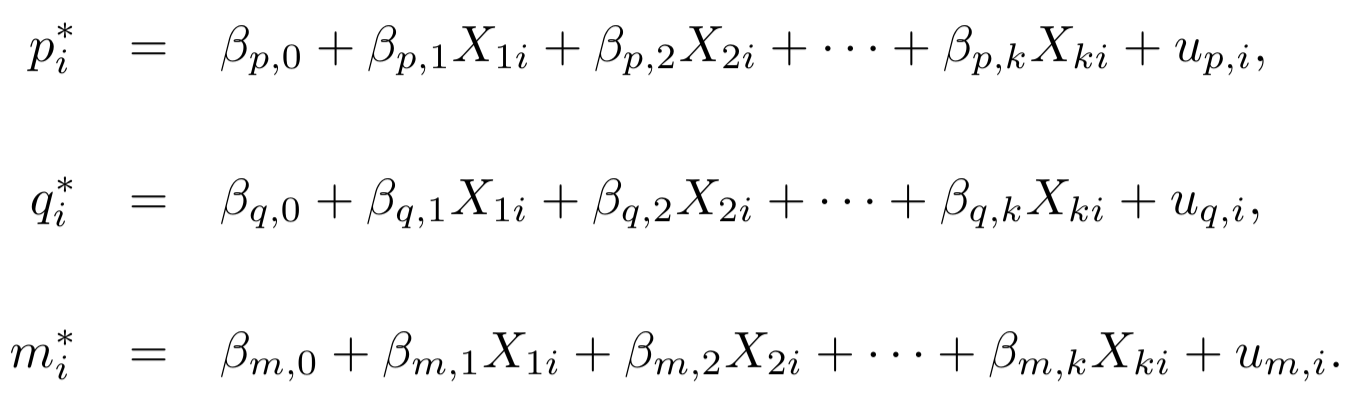“O passado está a nossa frente e o futuro em nossas costas”
Metáfora espacial para o tempo na cultura Aymara
Escrito por: Eduardo Pinheiro e Matheus Renzo
A previsão de lançamentos de novos produtos é uma tarefa desafiadora. A falta de dados do passado, assim como fatores desconhecidos que potencialmente podem influenciar no desempenho de novos produtos, tornam a estimação de performance nestes casos ainda mais difícil.
Apesar das dificuldades, a previsão de lançamentos é uma parte crucial para o planejamento de recursos, tal como uma ferramenta usada para avaliar o desempenho deste lançamento no futuro.
Metodologia
A abordagem é inspirada no modelo de difusão clássico proposto por Frank Bass em 1969, utilizado para descrever a adoção de novos produtos (principalmente na modelagem de curva de vendas acumulados em formato de S). Este modelo é caracterizado por 3 parâmetros: (m) potencial de mercado; (q) coeficiente de imitação e (p) coeficiente de influência externa. Que podem ser interpretados como o potencial de mercado para o produto lançamento (m), o efeito de fatores externos (ex: campanhas de marketing) no desempenho inicial (p) e a disseminação determinada pela recomendação de clientes que já consumiram o produto a consumidores em potencial (q).
Com isso, têm-se um modelo simples, computacionalmente barato e de bom desempenho preditivo, mas que ainda necessita de dados, pelos menos dos meses iniciais de venda. Mas como utilizá-lo para previsão da curva de lançamento se ainda não há vendas observadas? Bom, este produto já tem características estabelecidas: marca, data de lançamento, preço etc. Além disso, provavelmente há itens mais antigos com certo grau de similaridade. Uma alternativa, portanto, é estudar lançamentos passados similares e usá-los como referência para previsão das vendas do novo produto. Basicamente, pressupõe-se que se determinado produto X vendeu 1000 unidades durante os 12 primeiros meses um outro produto Y similar irá vender algo em torno disso no mesmo período.
Ok, mas como identificar um produto similar? e como usar curvas de lançamento passadas para previsão de novas? Basicamente, podemos ajustar o modelo de Bass para vendas de itens antigos, ajustar um modelo de regressão a fim de estudar a relação das curvas estimadas com as características dos produtos e por fim usar esse sistema de regressão para prever a curva de lançamento do novo item.
Mais formalmente, considere Y1, Y2, …, Yn como o conjunto de produtos antigos, cada um com suas respectivas características e dados de vendas. Seja Yh o novo produto. Considere o seguinte sistema de previsão:
1. Para cada produto será ajustado um modelo de Bass, em que serão estimados os respectivos parâmetros (p, q, m). Por exemplo, para o produto Y1 estima-se (p1, q1, m1).
2. Com isso, serão ajustados 3 modelos de regressão linear múltipla dados por:
em que
- (p*i, q*i, m*i) são os parâmetros estimados do modelo de Bass para para Yi.
- X1i, X2i, …, Xki são k características de Yi;
- β1 é o coeficiente de inclinação para X1, β2 o coeficiente de inclinação para X2 e assim por diante;
- ui é a fonte de variação no respectivo modelo de regressão.
3. Para Yh, iremos prever (ph, qh, mh) utilizando os respectivos modelos de regressão condicionados às características no novo item (X1h, X2h, …, Xkh).
Essencialmente, estamos utilizando um modelo de regressão para “estudar” a relação entre a curva de lançamento estimada caracterizada por (p, q e m) e as características dos produtos.
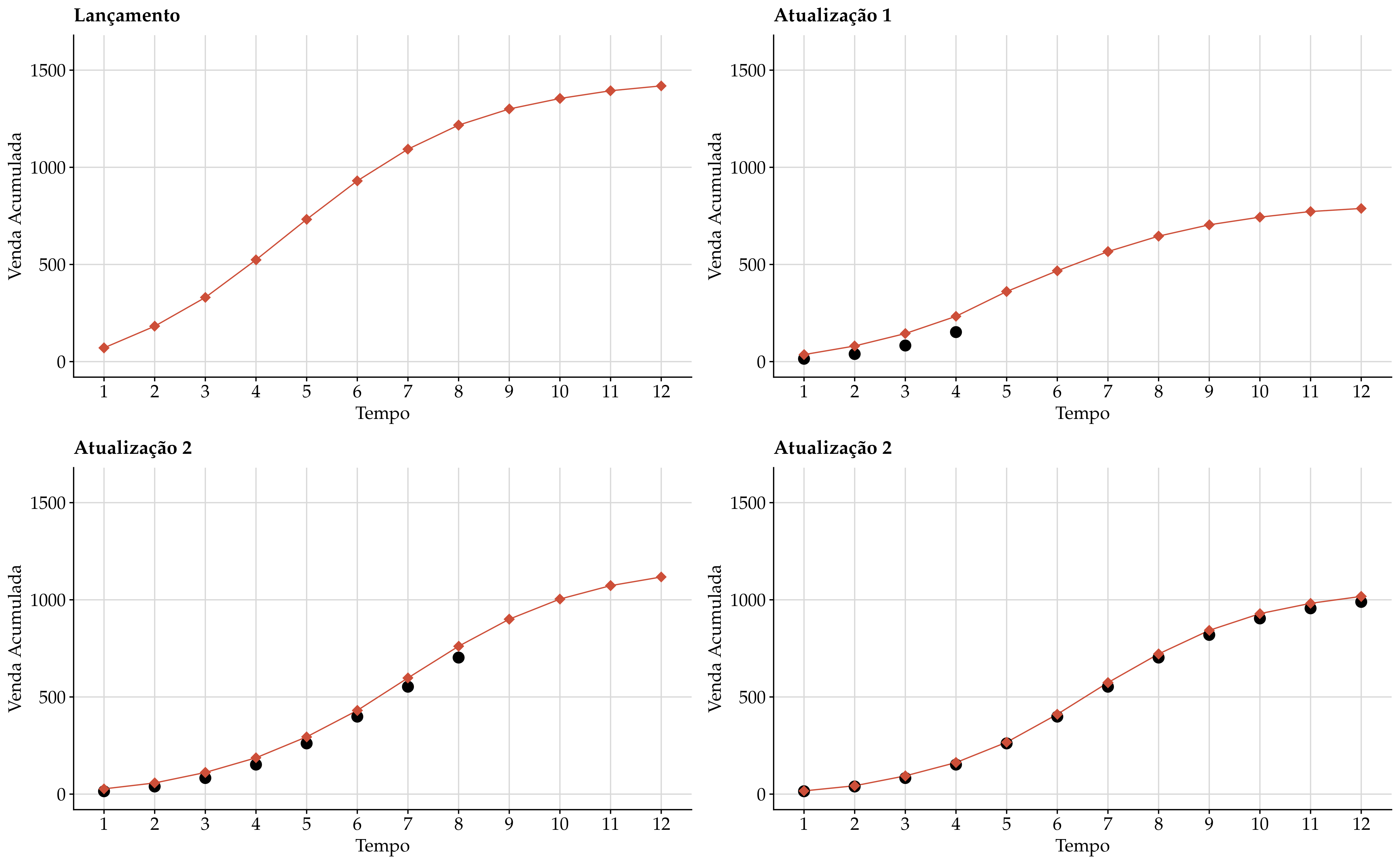
Dado isso, mais informação pode ser incorporada no sistema de previsão. Com a chegada de novos dados ainda pode ser útil a previsão de meses subsequentes; a curva de previsão construída considerando zero dados pode ser atualizada e se tornar mais assertiva. Para esta tarefa pode-se recorrer a inferência Bayesiana. Basicamente, para (ph, qh e mh) assumimos uma distribuição a priori t-student multivariada com v graus de liberdade, i.e
em que o vetor de médias e diagonal da matriz de variâncias e covariâncias a priori podem ser obtidos com os modelos de regressão supracitados. Supondo que Σ é uma matriz diagonal, supondo uma verossimilhança normal e considerando v=3 é possível por meio de MCMC obter a distribuição a posteriori de (ph, qh, mh) condicionada aos novos dados e assim uma curva de lançamento atualizada.
Com isso, têm-se um sistema capaz de realizar previsões para produtos que ainda serão lançados e posteriormente atualizá-las com a chegada de novos dados.