Escrito por: André Menezes.
Muito do que hoje em dia é divulgado pelo termo Inteligência Artificial nada mais é do que metodologias da matemática ou estatística que foram consolidadas e desenvolvidas em décadas passadas. Por exemplo, uma Inteligência Artificial que “encontra” o resultado ótimo sujeito a certas condições impostas pelo negócio, na sua essência é um tema abordado pela área da otimização/programação matemática.
Nesse contexto, a Murabei desenvolveu um desafio cujo objetivo era auxiliar na tomada de decisão sobre a redistribuição de recipientes retornáveis nas plantas de produção. Este projeto foi um desenvolvimento contínuo do case passado sobre previsão que pode ser encontrado aqui.
Desenvolvemos um algoritmo de otimização não linear inteira com recomendações semanais de movimentação (transferências e trocas) dos recipientes dentro do ecossistema da empresa. O ecossistema da empresa envolvia lugares (nós) com diferentes funções, especificamente:
- Plantas de produção: recebem os recipientes e também enviam para outras plantas.
- Centros de destroca: trocam os recipientes com as plantas de produção.
- Centros intermediários: enviam os recipientes para as plantas de produção.
- Centros de fabricação: fabricam e enviam os recipientes para as plantas de produção.
A relação entre os nós foi estabelecida de tal forma a levar em consideração as funções dos lugares, levando assim a um grafo, cuja variável de decisão foi definida como a quantidade de recipientes em lotes fixos que um caminhão pode transportar até alguma planta de produção. Enfatizamos que este problema, guardada as particularidades de cada empresa, está sistematizado e organizado em uma subárea da teoria da programação matemática conhecida como minimum-cost flow problem.
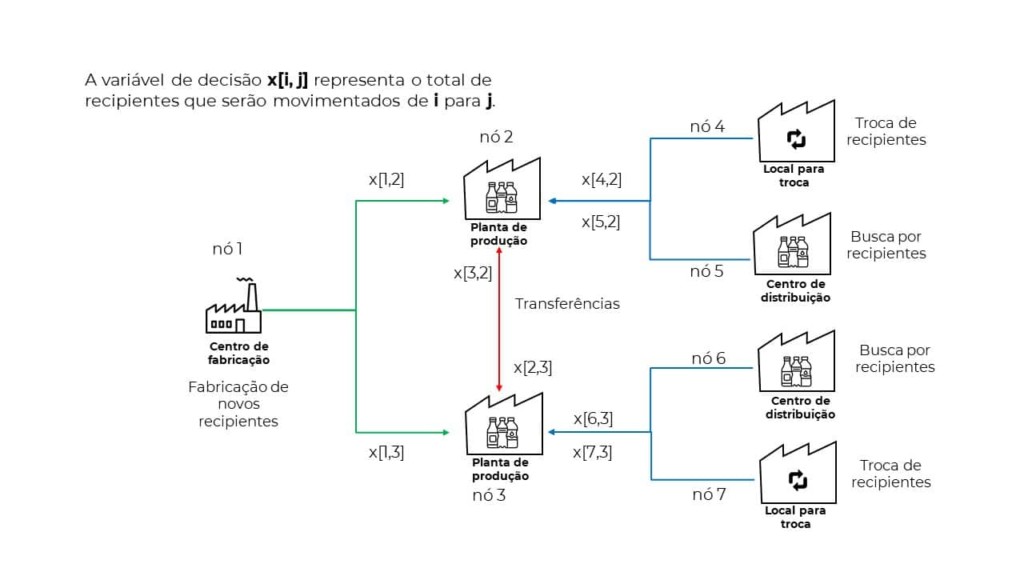
Outro elemento fundamental em problemas de otimização é a função objetivo. Neste desafio a função objetivo foi definida como a diferença entre o ganho de oportunidade e o custo de transporte. Usualmente, por questões de parcimônia e facilidade computacional, a função objetivo é uma função linear dos parâmetros e a variável de decisão. A fim de obter uma descrição mais realista do fenômeno, implementamos uma função objetivo não linear utilizando a técnica de piecewise linear function, ou seja, a função não linear é aproximada por segmentos de reta cuja a inclinação depende do nível de necessidade de cada planta de produção. Em outras palavras, o quão distante o total de recipientes na planta de produção está da demanda. Isso restringe que a planta de produção receba recipientes de forma infinita, mas até cumprir o seu nível de operação.
A Figura abaixo ilustra o comportamento da função objetivo piecewise linear. Note que a relação entre o ganho de oportunidade e o nível de oportunidade é uma curva, construída por segmentos de reta que atinge um platô. As inclinações das retas são controladas pelas faixas amarelas as quais são determinadas pela necessidade de recipientes de cada planta. Por outro lado, se a função objetivo fosse linear, o ganho de oportunidade aumentaria de forma infinita. Na prática o comportamento linear não faz sentido, pois nada garante que a planta vai conseguir ultrapassar a venda de recipientes muito além da sua real necessidade.
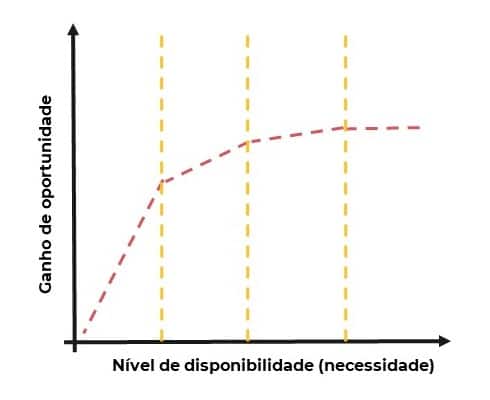
Como todo clássico problema de otimização, restrições foram implementadas de tal sorte a incorporar características do negócio. Por exemplo, a restrição de balanço de massa impõem que o total de recipientes que chegam até uma planta de produção não pode ser maior do que tem no lugar de origem.
Os resultados obtidos mostraram que a redistribuição de recipientes, seguindo as recomendações do modelo de otimização, se torna mais balanceada entre as plantas de produção, isto é, permitindo que cada planta tenha recipientes suficientes para operar de acordo com seu nível de demanda. O algoritmo também distribui recipientes de forma a priorizar lugares onde a necessidade de recipientes é bastante alarmante. Além disso, assumindo que as recomendações sejam realizadas nos cenários atuais da empresa, espera-se que o lucro diário aumente em duas vezes comparado com o lucro atual.
Alcançar uma visão anaĺítica dentro da sua empresa que permite auxiliar nas tomadas de decisões é de fundamental importância. O hype da vez é Inteligência Artificial e Machine Learning, mas mais importante que isso são cases de sucesso como esse da Murabei, onde conseguimos mostrar como modelos matemáticos podem ser ótimas ferramentas para suportar a tomada de decisão baseada em dados.
